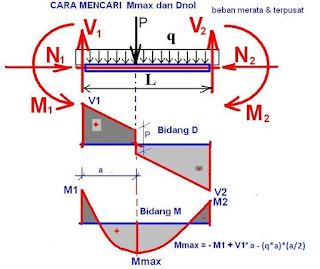
What are Free Body Diagrams?

One of the most useful aids for solving a statics problem is the free body
diagram (FBD). A free body diagram is a graphic, dematerialized, symbolic
representation of the body (structure, element or segment of an element)
in which all connecting "pieces" have been removed. A FBD is a
convenient method to model the structure, structural element, or segment
that is under scrutiny. It is a way in which to conceptualize the structure,
and its composite elements, so that an analysis may be initialized.
All of the physical attrributes of the structure are removed. This is not
completed at random, rather with a distinct method. A body, or segment thereof,
is represented by a simple single line. Each connection is solely represented
by a juncture with distinct properties, or is replaced by a set of forces
and moments which would represent the action at that connection. Internal
forces which would be found at a node (connection or joint) can be replaced
by representational external forces where that "part" connects
would connect with the other member in the FBD. All loads are represented
as force systems.

The image to the right is a link to a movie which illustrates the way in
which each of the loads on the structure (in this case the bench) are resolved.
It also illustrates how each and every physical load that acts upon the
structure must be represented. This means that all of the loads are replaced
by vectors. Even the supports are replaced by single vectors.
Notice how the person, cans and upper shelf dematerialize and are replaced
by vectors. The FBD at the end of the movie is not complete. What is missing?
Everything that is needed to solve a force system is included
on the FBD. Free body diagrams may not seem necessary in the relatively
simple current applications, but as problems become more complex, their
usefulness increases.

The following is the process for determining the reaction at the wall for
a cantilever beam. A FBD is first drawn of the beam. Next, cut the beam
free from the wall and replace the wall with the forces that were supporting
the beam at the wall before it was cut free. These forces are unknown, but
they are the only forces that can keep the beam in equilibrium. They are
identical to the internal forces in the beam at that point before it was
cut. The internal forces in the beam before it was cut free from its support
are also determined when the forces which will keep, or put, the FBD in
equilibrium are found.
A fixed support will resist translation in all directions
and rotation (moment). The FBD must show all of these directions. The principles
of equilibrium can always be used to solve a FBD. In the FBD above Sum Fy = 2K and Sum Fx = 0. The 2K forces
(load and vertical reaction force) cause a counter-clockwise couple of 10
K-FT which must be resisted by a moment on the end of the cut section of
10 K-FT acting in a clockwise direction.

This is an illustration of three different structural systems which have
one 100 pound load and one 150 pound load acting on them at exactly the
same point. They are also supported with a roller support at the left and
pinned support at the right. Each one could be a structure made of any type
of material.....wood, steel, bamboo, or perhaps paper.

This is a Free Body Diagram of these three systems which has been drawn
to represent the force system. Note how all of the internal structure has
been removed from this representation. The internal arrangement does not
matter for the determination of the supporting reactions! AND, if the supporting
and loading geometries are the same, the external reactions will alsways
remain the same.
The Umbrian Street Lamp 
This is a street lamp that is commonly found in Umbria, Italy. It looks
like many lamps found all over the world. The three photos illustrate how
the free body diagram for this structure should be conceived. The first
step is to dematerialize the lamp. Identify the center of the body and draw
this as a straght line. The only identifieable weight is the lamp, so this
is drawn as a vector as indicated. The next step is to determine what is
required at the other end of the lamp to maintain equilibrium; what is needed
to keep the lamp from spinning off into space? These forces (including the
moment) are drawn as indicated. What is missing from this illustration?
The magnitudes of the moment and force at the left side should be included
in a complete free body diagram.
The Verona Column 
There are many situations in which the exact conditions of the end restraints
are not able to be determined in the first glance. The materiality and relative
stiffness of the elements which are being supported/connected provide clues
as to the actual behavior.
This is a thin brick column supporting a wooden canopy at the old castle
in Verona, Italy. How is this element connected to the wall below?
Most likely one would model this behavior as a simple connection. The masonry
would have a very difficult time transferring moments since it cannot develop
the required tensile half of the couple. The mortar would also most likely
yield if a lateral load of significant force were to be applied. However,
one could argue that the column can, and certainly does, resist a small
amount of lateral load. And, due to the force of gravity pulling each brick
down there could be the possibility for the base to begin to resist a moderate
moment as long as the tensile force does not exceed the compressive force
due to the self-weight of the structure. So, where does this leave the FBD?
In the hands of the designer to make a choice on the type of model that
he/she desires.... What is the correct model? It depends.
Apa yang dimaksud 'Free body diagram' ?
 Salah satu alat bantu yang paling berguna untuk memecahkan masalah statika adalah diagram benda bebas (FBD).
Diagram benda bebas adalah, grafis dematerialized, representasi
simbolis dari tubuh (struktur, elemen atau segmen elemen) di mana semua
menghubungkan "potongan" telah dihapus. FBD adalah metode yang nyaman untuk model struktur, elemen struktur, atau segmen yang berada di bawah pengawasan. Ini adalah cara di mana untuk konsep struktur, dan elemen komposit, sehingga analisis dapat diinisialisasi.
Semua attrributes fisik dari struktur dihapus. Hal ini tidak diselesaikan secara acak, bukan dengan metode yang berbeda. Sebuah badan, atau segmen daripadanya, diwakili oleh garis tunggal yang sederhana.
Setiap koneksi hanya diwakili oleh titik dengan sifat yang berbeda,
atau digantikan oleh seperangkat kekuatan dan momen yang akan mewakili
aksi di koneksi.
Kekuatan internal yang akan ditemukan pada simpul (koneksi atau sendi)
dapat digantikan oleh kekuatan eksternal representasional mana yang
"bagian" menghubungkan akan menghubungkan dengan anggota lain dalam FBD
tersebut. Semua beban yang direpresentasikan sebagai sistem gaya.
Salah satu alat bantu yang paling berguna untuk memecahkan masalah statika adalah diagram benda bebas (FBD).
Diagram benda bebas adalah, grafis dematerialized, representasi
simbolis dari tubuh (struktur, elemen atau segmen elemen) di mana semua
menghubungkan "potongan" telah dihapus. FBD adalah metode yang nyaman untuk model struktur, elemen struktur, atau segmen yang berada di bawah pengawasan. Ini adalah cara di mana untuk konsep struktur, dan elemen komposit, sehingga analisis dapat diinisialisasi.
Semua attrributes fisik dari struktur dihapus. Hal ini tidak diselesaikan secara acak, bukan dengan metode yang berbeda. Sebuah badan, atau segmen daripadanya, diwakili oleh garis tunggal yang sederhana.
Setiap koneksi hanya diwakili oleh titik dengan sifat yang berbeda,
atau digantikan oleh seperangkat kekuatan dan momen yang akan mewakili
aksi di koneksi.
Kekuatan internal yang akan ditemukan pada simpul (koneksi atau sendi)
dapat digantikan oleh kekuatan eksternal representasional mana yang
"bagian" menghubungkan akan menghubungkan dengan anggota lain dalam FBD
tersebut. Semua beban yang direpresentasikan sebagai sistem gaya.
 Gambar ke kanan adalah link ke sebuah film yang menggambarkan cara di
mana masing-masing beban pada struktur (dalam hal ini bangku)
diselesaikan. Hal ini juga menggambarkan bagaimana masing-masing dan setiap beban fisik yang bertindak pada struktur harus diwakili. Ini berarti bahwa semua beban yang digantikan oleh vektor. Bahkan mendukung digantikan oleh vektor tunggal.
Gambar ke kanan adalah link ke sebuah film yang menggambarkan cara di
mana masing-masing beban pada struktur (dalam hal ini bangku)
diselesaikan. Hal ini juga menggambarkan bagaimana masing-masing dan setiap beban fisik yang bertindak pada struktur harus diwakili. Ini berarti bahwa semua beban yang digantikan oleh vektor. Bahkan mendukung digantikan oleh vektor tunggal.
Perhatikan bagaimana orang, kaleng dan rak atas dematerialize dan digantikan oleh vektor. Para FBD di akhir film tidak lengkap. Apa yang hilang?
Segala sesuatu yang diperlukan untuk memecahkan suatu sistem gaya disertakan pada FBD tersebut.
Diagram benda bebas mungkin tidak diperlukan dalam aplikasi saat ini
relatif sederhana, tetapi sebagai masalah menjadi lebih kompleks,
meningkatkan kegunaan mereka.

Berikut ini adalah proses untuk menentukan reaksi pada dinding untuk balok kantilever. FBD adalah pertama ditarik dari balok.
Selanjutnya, potong balok bebas dari dinding dan mengganti dinding
dengan kekuatan-kekuatan yang mendukung balok pada dinding sebelum
dipotong gratis. Kekuatan ini tidak diketahui, tetapi mereka satu-satunya pasukan yang dapat menjaga balok dalam kesetimbangan. Mereka identik dengan kekuatan-kekuatan internal dalam berkas pada titik bahwa sebelum itu dipotong.
Kekuatan-kekuatan internal dalam berkas sebelum dipotong bebas dari
dukungan juga ditentukan ketika pasukan yang akan tetap, atau
meletakkan, FBD dalam kesetimbangan ditemukan.
Sebuah dukungan tetap akan menolak terjemahan dalam segala arah dan rotasi (momen). FBD harus menunjukkan semua arah. Prinsip-prinsip keseimbangan selalu dapat digunakan untuk memecahkan suatu FBD. Dalam FBD atas Sum F y = 2K dan Sum F x = 0.
Pasukan 2K (beban dan gaya reaksi vertikal) menyebabkan pasangan
berlawanan arah jarum jam dari 10 K-FT yang harus dilawan oleh sejenak
di akhir bagian yang dipotong dari 10 K-FT bertindak searah jarum jam.

Ini adalah sebuah ilustrasi dari tiga sistem struktur yang berbeda yang
memiliki satu beban 100 kilo dan satu kilo 150 beban yang bekerja pada
mereka tepat pada titik yang sama. Mereka juga didukung dengan dukungan rol pada dukungan kiri dan ditempelkan di sebelah kanan. Masing-masing bisa menjadi struktur dibuat dari setiap jenis material ..... kayu, baja, bambu, atau mungkin kertas.

Ini adalah diagram benda bebas dari ketiga sistem yang telah ditarik untuk mewakili sistem gaya. Perhatikan bagaimana semua struktur internal telah dihapus dari representasi ini. Pengaturan internal tidak peduli untuk penentuan reaksi mendukung! DAN, jika geometri mendukung dan loading sama, reaksi eksternal alsways akan tetap sama.
Para Umbrian Lampu Jalan 
Ini adalah lampu jalanan yang umum ditemukan di Umbria, Italia. Ini terlihat seperti lampu banyak ditemukan di seluruh dunia. Tiga foto menggambarkan bagaimana diagram benda bebas untuk struktur ini harus dipahami. Langkah pertama adalah untuk dematerialize lampu. Mengidentifikasi pusat tubuh dan imbang ini sebagai garis straght. Berat hanya identifieable adalah lampu, jadi ini digambar sebagai vektor seperti yang ditunjukkan.
Langkah berikutnya adalah untuk menentukan apa yang diperlukan pada
ujung lampu untuk mempertahankan ekuilibrium; apa yang dibutuhkan untuk
menjaga lampu dari berputar ke angkasa? Kekuatan ini (termasuk saat ini) diambil seperti ditunjukkan. Apa yang hilang dari ilustrasi ini? Besaran momen dan kekuatan di sisi kiri harus dimasukkan dalam diagram tubuh lengkap gratis.
Verona Kolom 
Ada banyak situasi di mana kondisi yang tepat dari pengekangan akhir tidak dapat ditentukan pada pandangan pertama. Materialitas dan kekakuan relatif dari unsur-unsur yang didukung / terhubung memberikan petunjuk pada perilaku aktual.
Ini adalah kolom batu bata tipis mendukung kanopi kayu di kastil tua di Verona, Italia. Bagaimana elemen ini terhubung ke dinding di bawah?
Salah satu kemungkinan besar akan model perilaku ini sebagai koneksi sederhana.
Batu akan memiliki waktu yang sangat sulit mentransfer saat karena
tidak dapat mengembangkan setengah tarik yang dibutuhkan pasangan. Mortir tersebut juga akan menghasilkan kemungkinan besar jika beban lateral kekuatan yang signifikan itu harus diterapkan. Namun, orang dapat berargumentasi bahwa kolom dapat, dan tentu saja, menolak sejumlah kecil beban lateral.
Dan, karena gaya gravitasi menarik setiap batu bata di sana bisa
menjadi kemungkinan dasar untuk mulai menolak saat moderat selama gaya
tarik tidak melebihi gaya tekan karena berat diri-struktur. Jadi, mana ini meninggalkan FBD itu? Di tangan desainer untuk membuat pilihan pada jenis model yang ia / dia inginkan .... Apa model yang benar? Itu tergantung.
Sumber :
http://web.mit.edu/4.441/1_lectures/1_lecture14/1_lecture14.html